Rumus Simpangan Baku, Simpangan rata-rata, Ragam, Variansi, Koefisen Keragaman, Contoh Soal, Data Tunggal Kelompok, Jawaban, Statistik, Matematika - Berikut ini adalah materi lengkap simpangan baku, simpangan rata-rata, ragam, variansi, dan koefisen keragaman :
Sekumpulan data kuantitatif yang tidak dikelompokkan dinyatakan oleh x1, x2, …, xn. Dari data tersebut dapat ditentukan simpangan rata-rata (SR) dengan menggunakan rumus :
Contoh Soal 1
Hitung simpangan rata-rata dari data kuantitatif berikut :
12, 3, 11, 3, 4, 7, 5, 11
Pembahasan 1
Jadi, simpangan rata-ratanya adalah 3,25.
Coba Anda tentukan simpangan rata-rata tersebut dengan menggunakan kalkulator. Apakah hasilnya sama?
Untuk sekumpulan data yang dinyatakan oleh x1, x2, …, xn dan masing-masing nilai data tersebut mempunyai frekuensi f1 , f2 , …, fn diperoleh nilai simpangan rata-rata (SR) dengan menggunakan rumus:
Contoh Soal 2
Hitunglah simpangan rata-rata nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka seperti Tabel 1.
Tabel 1. Nilai ulangan Fisika dari siswa Kelas XI SMA Merdeka
Interval Kelas
|
Frekuensi
|
40 – 44
|
3
|
45 – 49
|
4
|
50 – 54
|
6
|
55 – 59
|
8
|
60 – 64
|
10
|
65 – 69
|
11
|
70 – 74
|
15
|
75 – 79
|
6
|
80 – 84
|
4
|
85 – 89
|
2
|
90 – 94
|
2
|
Penyelesaian 2
Kelas
Interval
|
Nilai Tengah (xi)
|
fi
| ||
40 – 44
|
42
|
3
|
23,7
|
71,1
|
45 – 49
|
47
|
4
|
18,7
|
74,8
|
50 – 54
|
52
|
6
|
13,7
|
82,2
|
55 – 59
|
57
|
8
|
8,7
|
69,6
|
60 – 64
|
62
|
10
|
3,7
|
37
|
65 – 69
|
67
|
11
|
1,3
|
14,3
|
70 – 74
|
72
|
15
|
6,3
|
94,5
|
75 – 79
|
77
|
6
|
11,3
|
67,8
|
80 – 84
|
82
|
4
|
16,3
|
65,2
|
85 – 89
|
87
|
2
|
21,3
|
42,6
|
90 – 94
|
92
|
2
|
26,3
|
52,6
|
Σfi = 71
|
Jadi, simpangan rata-rata (SR) = 671,7 / 71 = 9,46.
Ingatlah :
Simpangan rataan hitung menunjukkan rataan hitung jauhnya datum dari rataan hitung.
Untuk menghitung simpangan baku dari data kuantitatif: 2, 5, 7, 4, 3, 11, 3 dengan kalkulator ilmiah (fx–3600Pv) adalah sebagai berikut
1)
|
Kalkulator “ON”
| |
2)
|
MODE 3 → Program SD
| |
3)
|
Masukkan data
| |
2 data
| ||
5 data
| ||
…
| ||
…
| ||
…
| ||
3 data
| ||
4)
|
Tekan tombol x αn-1
| |
α = 2,878491669 = 2,88
| ||
Diketahui sekumpulan data kuantitatif yang tidak dikelompokkan dan dinyatakan oleh x1, x2, …, xn. Dari data tersebut, dapat diperoleh nilai simpangan baku (S) yang ditentukan oleh rumus berikut.
Contoh Soal 3
Dari 40 orang siswa diambil sampel 9 orang untuk diukur tinggi badannya, diperoleh data berikut:
165, 170, 169, 168, 156, 160, 175, 162, 169.
Hitunglah simpangan baku sampel dari data tersebut.
Kunci Jawaban 3
Jadi, simpangan bakunya adalah 5,83.
Sekumpulan data kuantitatif yang dikelompokkan, dapat dinyatakan oleh x1, x2, …, xn dan masing-masing data mempunyai frekuensi f1, f2, …, fn. Simpangan baku (S) dari data tersebut diperoleh dengan menggunakan rumus :
Contoh Soal 4
Hitunglah simpangan baku dari nilai ulangan Fisika dari 71 siswa kelas XI SMA Merdeka sesuai Tabel 1.
Jawaban 4
Dari hasil perhitungan sebelumnya diperoleh µ = 65,7.
xi
|
fi
|
xi - µ
|
(xi - µ)2
|
Σfi (xi - µ)2
|
42
|
3
|
–23,7
|
561,69
|
1.685,07
|
47
|
4
|
–18,7
|
349,69
|
1.398,76
|
52
|
6
|
–13,7
|
187,69
|
1.126,14
|
57
|
8
|
– 8,7
|
75,69
|
605,52
|
62
|
10
|
–3,7
|
13,69
|
136,9
|
67
|
11
|
1,3
|
1,69
|
18,59
|
72
|
15
|
6,3
|
39,69
|
595,35
|
77
|
6
|
11,3
|
127,69
|
766,14
|
82
|
4
|
16,3
|
265,69
|
1.062,76
|
87
|
2
|
21,3
|
453,69
|
907,38
|
92
|
2
|
26,3
|
691,69
|
1.383,38
|
Σfi = 60
|
Σfi (xi - µ)2 = 9.685,99
|
Jadi, simpangan bakunya σ :
3. Variansi (Ragam)
Untuk data yang tidak dikelompokkan ataupun data yang dikelompokkan, diperoleh nilai variansi (v) dengan
menggunakan rumus:
Contoh Soal 5
Hitunglah variansi dari data Contoh 3.
Pembahasan :
Dari hasil perhitungan Contoh 3. diperoleh S = 5,83 maka :
v = S2 = (5,83)2 = 33,99.
5. Koefisien Keragaman (KK)
Rumus koefisien keragaman (KK) dari sekumpulan data x1, x2, x3 …, xn. adalah :
Dalam hal ini,
S = simpangan baku
x = rataan
Contoh Soal 6
Pak Murtono seorang pengusaha. Bidang usaha yang ia jalani adalah penerbitan, tekstil, dan angkutan. Dalam 5 bulan terakhir, ia mencatat keuntungan bersih ketiga bidang usahanya. Hasilnya tampak pada Tabel 2.
Tabel 2. Keuntungan Bersih Usaha Pak Murtono Selama 5 Bulan Terakhir.
Bidang Usaha
|
Keuntungan Bersih (dalam puluhan juta rupiah)
| ||||
Bulan ke-1
|
Bulan ke-2
|
Bulan ke-3
|
Bulan ke-4
|
Bulan ke-5
| |
Penerbitan
|
60
|
116
|
100
|
132
|
72
|
Tekstil
|
144
|
132
|
108
|
192
|
204
|
Angkutan
|
80
|
260
|
280
|
72
|
116
|
Jika Pak Murtono berpendapat bahwa bidang usaha yang akan dipertahankan hanya dua bidang usaha dengan kriteria bidang usaha dengan keuntungan bersih yang stabil, tentukanlah bidang usaha yang sebaiknya tidak dilanjutkan.
Jawaban 6
Langkah ke-1 :
Menuliskan apa yang diketahui dan apa yang ditanyakan soal tersebut.
Diketahui :
• keuntungan bersih selama 5 bulan terakhir yang disajikan pada Tabel 2.
• bidang usaha yang dipertahankan adalah yang memiliki keuntungan bersih yang stabil.
Ditanyakan: bidang usaha yang sebaiknya tidak dilanjutkan.
Langkah ke-2 :
Menentukan konsep yang akan digunakan dalam menyelesaikan soal. Pada soal ini, konsep yang digunakan adalah rataan, simpangan baku, dan koefisien keragaman.
Langkah ke-3 :
Menghitung rataan, simpangan baku, dan koefisien keragaman dari setiap bidang usaha.
→ Bidang usaha penerbitan
KK = S/x = 29,93/ 96 = 0,31
→ Bidang usaha tekstil
x =156
S = 40,69
KK = S/x = 40,69/156 = 0,26
→ Bidang usaha angkutan
x = 161,6
S = 100.58
KK = S/x = 100,58/161,6 = 0,62
Jadi, sebaiknya Pak Murtono tidak melanjutkan usaha angkutan karena keuntungannya tidak stabil (nilai KK paling besar).
Anda sekarang sudah mengetahui Simpangan Baku dan Simpangan rata-rata. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.
Referensi :
Djumanta, W. 2008. Mahir Mengembangkan Kemampuan Matematika 2 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah. Pusat Perbukuan, Departemen Pendidikan Nasional, Jakarta. p. 250.







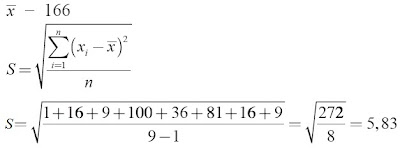






Tidak ada komentar:
Posting Komentar